Research conducted by the Variational AI team: Marshall Drew-Brook, Peter Guzzo, Ahmad Issa, Mehran Khodabandeh, Sara Omar, Jason Rolfe, and Ali Saberali.
Searching through the space of synthesizable molecules to find an effective drug candidate is one of the most time-consuming and expensive steps of drug discovery. Once a protein mediating disease has been identified and some initial hits that weakly modulate the target have been found, this structure- and ligand-based information must bootstrap the hunt for a potent, selective, ADMET-compliant drug candidate. The associated hit-to-lead and lead optimization process takes multiple years and many millions of dollars (Paul, et al., 2010), driven by the large number of novel molecules that must be investigated to converge to a satisfactory drug candidate, and the cost of synthesizing each such molecule along the way.
Artificial intelligence has the potential to accelerate hit-to-lead and lead optimization by reducing the number of novel compounds required to find a drug candidate. We show how active learning using Variational AI’s generative foundation model, Enki, can find extremely potent compounds for a novel target with data on only 500 molecules. Used in conjunction with absolute binding free energy (ABFE) calculations, Enki promises to identify potent, selective leads in mere weeks, and converge to a promising drug candidate in a few additional rounds of experimental synthesis and testing.To reconcile the disparity in generalization between QSAR and conventional machine learning tasks, we need to identify its cause. Three potential explanations present themselvesIn a succession of posts, we will explore each of these possibilities in turn, beginning with the first.
Active learning is the AI embodiment of the design-make-test-analyze cycle
Hit-to-lead and lead optimization are generally conducted via the design-make-test-analyze (DMTA) cycle. In each cycle (starting with “A”), the available experimental data is first analyzed. For instance, structure-activity relationships are characterized based upon series of molecules in which a single feature has been varied (e.g., ring size). New compounds are then designed by tuning molecular features that exhibit a consistent relationship with potency, selectivity, or other pharmacological properties, to their optimal values. These compounds are synthesized (made), tested, and used as the basis for further investigation.
The DMTA cycle is an instance of active learning (or more precisely, Bayesian optimization), an AI paradigm for optimizing an objective (e.g., a weighted combination of potency, selectivity, and ADMET) by iteratively selecting points (e.g., molecules) for evaluation (Shahriari, et al., 2015). Bayesian optimization must balance exploration (e.g., of novel chemotypes) with exploitation (e.g., of previously identified potent scaffolds). The most effective Bayesian optimization algorithms explicitly model the uncertainty of predictions, and use the predicted uncertainty to maximize rigorous measures of search quality such as the expected improvement (Gómez-Bombarelli, et al., 2018; Griffiths & Hernández-Lobato, 2020). However, more heuristic approaches such as reinforcement learning (Olivecrona, et al., 2017), genetic algorithms (Jensen, 2019), and particle swarm optimization (Winter, et al., 2019) can also be used.

Figure 1: The conventional DMTA cycle can be automated with Enki’s generative foundation model.
Enki performs active learning via Bayesian optimization on a powerful, generative foundation model, pretrained on millions of potency data points across hundreds of targets. This allows it to find extremely potent ligands for a novel target, given target activity data on only 500 molecules, spread across five rounds DMTA/active learning. On each round of active learning, we fine-tune Enki on the available data for the novel target, and then search over the full space of synthesizable, drug-like molecules to find those that maximize the expected improvement of the predicted potency.
Flexible architectures are almost unbeatable
We evaluate Enki’s ability to optimize potency against three kinase targets of significant pharmacological interest: FGFR1, AURKA, and EGFR. While these are familiar drug targets, we render them novel for the purpose of this benchmark by removing all data on them, and all other targets with more than 65% homology, from the pretraining data. We then maximize pIC50 – 3*(1-QED), where QED is the quantitative estimate of drug-likeness (Bickerton, et al., 2012). The scale of the QED term is chosen to ensure that the best compounds in a 2.2M molecule screening set approximately satisfy Lipinski’s Rule of 5.
Enki is initially fine-tuned on the potency of 100 randomly selected molecules against the optimization target. (The source library is the same used for high-throughput screening, described below.) In each of five succeeding rounds of active learning, Enki generates 100 molecules for potency evaluation that maximize the expected improvement of the predicted potency, and is fine-tuned to incorporate this data.
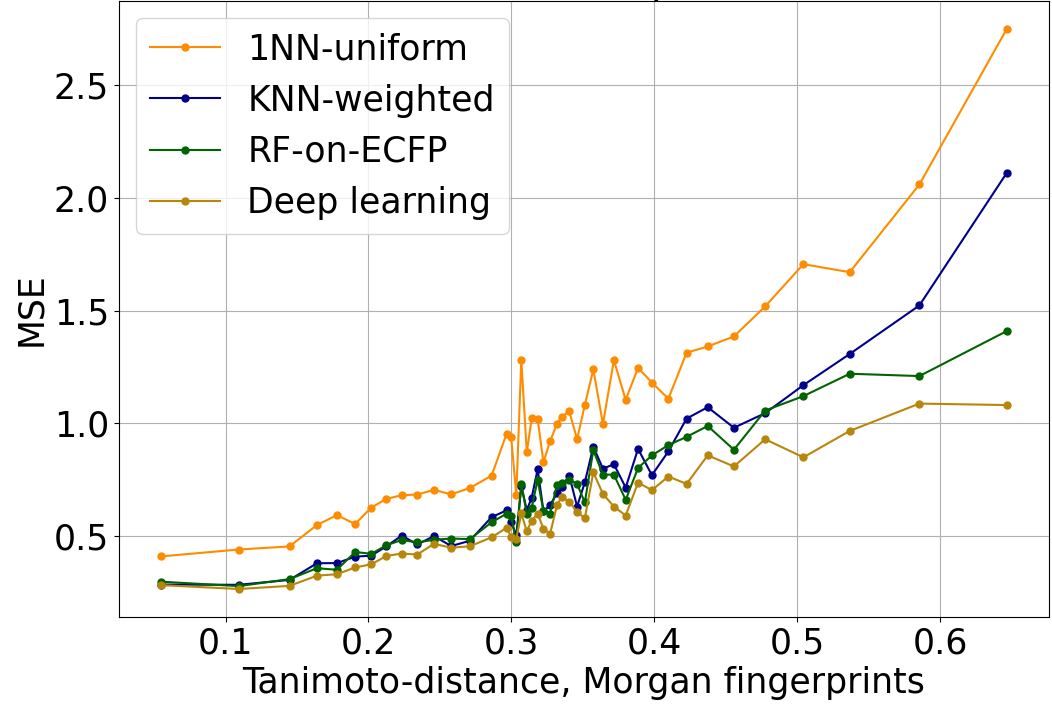
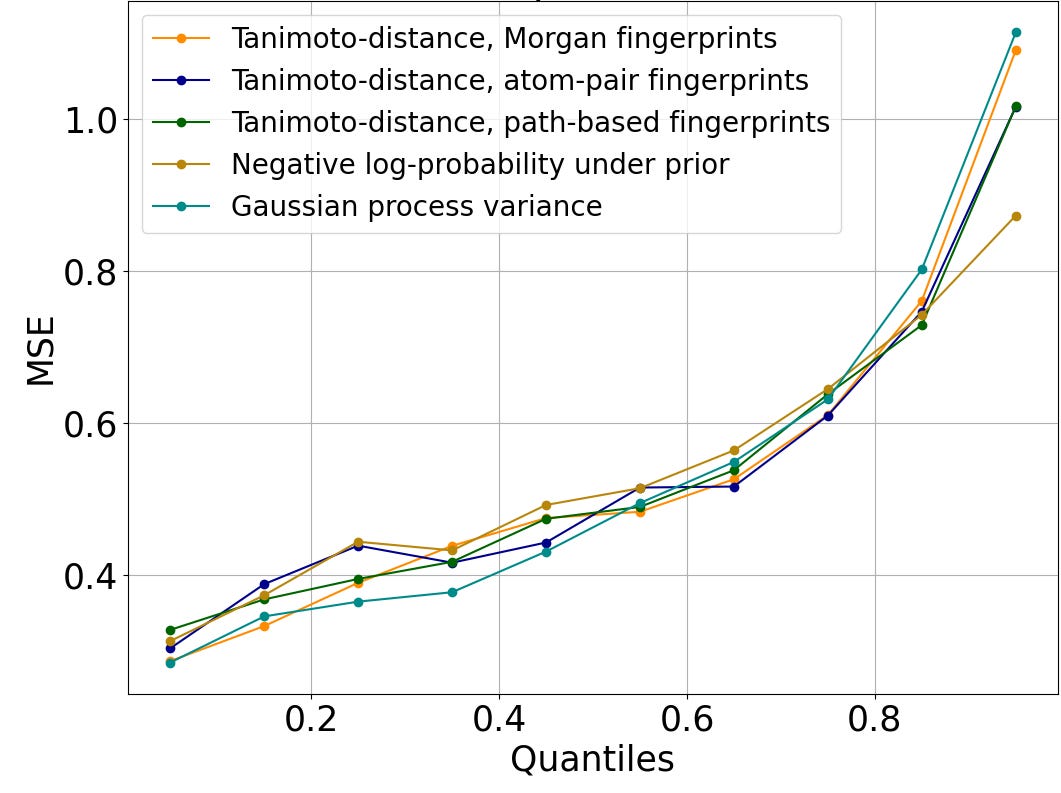
We compare Enki to REINVENT (Olivecrona, et al., 2017; Loeffler, et al., 2024) and graph genetic algorithms (Graph GA; Jensen, 2019), the previous state-of-the-art in molecular optimization as determined by extensive benchmarking (Gao, et al., 2022; Nigam, et al., 2024). To adapt REINVENT and Graph GA to real-world lead optimization, where only a few novel molecules can be tested experimentally in each round of active learning, we equipped them with a QSAR model consisting of a random forest regressor operating on extended connectivity fingerprints (Dodds, et al., 2024; Nahal, et al., 2024). This architecture continues to achieve competitive performance for small molecule potency prediction (Cichońska, et al., 2021; Huang, et al., 2021; Luukkonen, et al., 2023; Stanley, et al., 2021; van Tilborg, et al., 2022).
To facilitate fast and cost-effective benchmarking, we use molecular docking as a proxy for (not an approximation to) experimental potency. We treat docking scores as the true target endpoint, on the principle that if we can optimize docking scores using docking data, we should also be able to optimize experimental potencies using experimental data. As we have discussed in a previous post, molecular docking scores are a natural surrogate for experimental potencies because they are based upon the same geometry of pharmacophoric interactions that mediate experimental potency, are correlated with experimental potency, and are almost as difficult to predict as experimental potency. The docking scores are computed using Gnina’s CNNaffinity, a machine learning scoring function that is calibrated to pIC50 (McNutt, et al., 2021).
We also compare to high-throughput screening by evaluating the true objective value for ~1.3M molecules that have previously been experimentally tested for kinase activity, ~0.4M molecules that have been tested for activity for other target classes, and ~0.5M molecules from the Enamine, WuXi, Otava, and Mcule make-on-demand sets. Half of the make-on-demand molecules were constrained to have a hinge binding scaffold, which is typical of kinase inhibitors. This library is biased towards compounds that are likely to bind to our targets, and thus represents a rigorous baseline for Enki.
Flexible architectures are almost unbeatable
The performance of active learning with Enki on three novel targets, compared to a high-throughput screen, is depicted in Figures 2 and 3. In all cases, the best of the Enki-optimized molecules is superior to any of the ~2M high-throughput screening molecules.
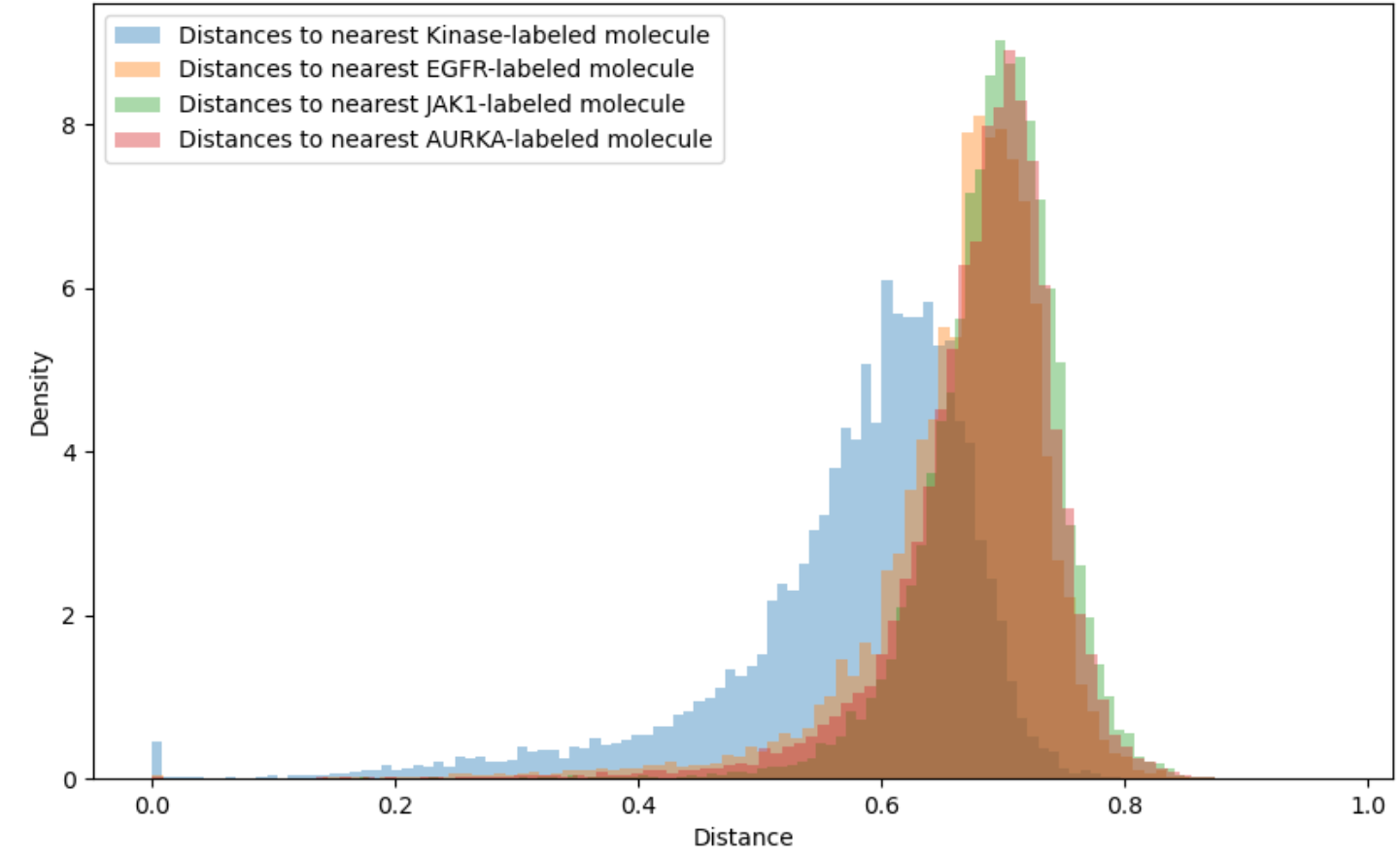
The Enki-optimized molecules are novel relative to the 100 random molecules used to initialize active learning, as demonstrated in Figures 4, 5, and 6. We also evaluated synthesizability by performing retrosynthetic pathway prediction using Molecule.one. The distribution of the predicted number of synthetic steps is shown in Figure 7. For all three tasks, 90% of the Enki-optimized molecules were predicted to be synthesizable in fewer than ten steps.
We compared Enki, REINVENT, and Graph GA across five rounds of active learning, each comprising 100 molecules. As Figures 8 and 9 show, Enki produces molecules that better satisfy the optimization objective: pIC50 – 3*(1 – QED). These differences are highly statistically significant, with a large or very large effect size in all but one case (Table 1). Enki drives potency (CNNaffinity) to very high levels, significantly surpassing REINVENT and Graph GA as measured by both the mean over all 100 molecules in the last round of active learning, as well as when only considering the best molecules (Figure 10). In contrast, REINVENT and Graph GA over-optimize QED, driving it to excessive levels at the expense of potency (Figure 11). Enki’s effective potency optimization can be understood in terms of binding interactions in the docked poses (Figure 12).

Figure 2: Distribution of the optimization objective values over high-throughput screening libraries, and Enki-optimized molecules from the fifth round of active learning, for the three benchmark tasks.

Figure 3: Distribution of the optimization objective values over high-throughput screening libraries, and Enki-optimized molecules from the fifth round of active learning, for the three benchmark tasks, zoomed to highlight the best molecules.

Figure 4: Examples of Enki-optimized molecules from the fifth round of active learning for FGFR1 potency, along with the most similar molecules in the set of 100 molecules used to initialize optimization.

Figure 5: Examples of Enki-optimized molecules from the fifth round of active learning for AURKA potency, along with the most similar molecules in the set of 100 molecules used to initialize optimization.

Figure 6: Distribution of Tanimoto similarity of Enki-optimized molecules from the fifth round of active learning to the nearest molecule in the initial set of 100 molecules for the three benchmark tasks.

Figure 7: Distribution of number of synthetic steps predicted by retrosynthetic pathway prediction for Enki-optimized molecules from the fifth round of active learning.

Figure 8: Evolution of the optimization objective over five rounds of active learning using Enki, REINVENT, and Graph GA. Centerline, box, and whiskers indicate median, 25/75th percentile, 3/97th percentile, respectively. Additional points denote outliers beyond that range. For all targets, the round-5 Enki-optimized compounds are superior to those produced by REINVENT and Graph GA with p < 0.005 according to the Mann-Whitney U test.

Figure 9: Distribution of the optimization objective for Enki, REINVENT, and Graph GA-optimized molecules from the fifth round of active learning. The mean of each distribution is denoted by a dotted line.

Table 1: Statistical comparison of molecules from the fifth round of active learning produced by Enki, compared to REINVENT and Graph GA. P-values are computed using the Mann-Whitney U test and effect sizes are evaluated using Cohen’s d. d = 0.2 is considered a small effect size, d=0.5 is medium, d=0.8 is large, and 1.2 is very large.

Figure 10: Distribution of the docking score (potency) for Enki, REINVENT, and Graph GA-optimized molecules from the fifth round of active learning. The mean of each distribution is denoted by a dotted line.

Figure 11: Distribution of QED (quantitative estimate of drug-likeness) for Enki, REINVENT, and Graph GA-optimized molecules from the fifth round of active learning. The mean of each distribution is denoted by a dotted line.

Figure 12: Evolution of ligand-protein interactions over multiple rounds of active learning with Enki.
Efficient application of active learning in practice
While active learning can be directly applied to experimental potency measurements, repeated rounds of unconstrained optimization over synthesizable, drug-like chemical space is time consuming and expensive. Even tractable de novo molecules can require months of effort and thousands of dollars to synthesize. Early rounds of active learning can be conducted more efficiently using computational approximations: first molecular docking, and then absolute binding free energy computations via free energy perturbations or thermodynamic integration.
The results presented here suggest that active learning with Enki should converge to extremely potent ligands, as predicted by ABFE, with only a few hundred evaluations. Computation on this scale can be easily completed within a week on a moderately sized cluster. The compounds can then be synthesized and tested, and used to seed a few final rounds of active learning based upon experimental data.
References
Bickerton, G. R., Paolini, G. V., Besnard, J., Muresan, S., & Hopkins, A. L. (2012). Quantifying the chemical beauty of drugs. Nature chemistry, 4(2), 90-98.
Cichońska, A., Ravikumar, B., Allaway, R. J., Wan, F., Park, S., Isayev, O., … & Challenge organizers. (2021). Crowdsourced mapping of unexplored target space of kinase inhibitors. Nature communications, 12(1), 3307.
Dodds, M., Guo, J., Löhr, T., Tibo, A., Engkvist, O., & Janet, J. P. (2024). Sample efficient reinforcement learning with active learning for molecular design. Chemical Science, 15(11), 4146-4160.
Gao, W., Fu, T., Sun, J., & Coley, C. (2022). Sample efficiency matters: a benchmark for practical molecular optimization. Advances in neural information processing systems, 35, 21342-21357.
Gómez-Bombarelli, R., Wei, J. N., Duvenaud, D., Hernández-Lobato, J. M., Sánchez-Lengeling, B., Sheberla, D., … & Aspuru-Guzik, A. (2018). Automatic chemical design using a data-driven continuous representation of molecules. ACS central science, 4(2), 268-276.
Griffiths, R. R., & Hernández-Lobato, J. M. (2020). Constrained Bayesian optimization for automatic chemical design using variational autoencoders. Chemical science, 11(2), 577-586.
Huang, K., Fu, T., Gao, W., Zhao, Y., Roohani, Y., Leskovec, J., … & Zitnik, M. (2021). Therapeutics data commons: Machine learning datasets and tasks for drug discovery and development. arXiv preprint arXiv:2102.09548.
Jensen, J. H. (2019). A graph-based genetic algorithm and generative model/Monte Carlo tree search for the exploration of chemical space. Chemical science, 10(12), 3567-3572.
Loeffler, H. H., He, J., Tibo, A., Janet, J. P., Voronov, A., Mervin, L. H., & Engkvist, O. (2024). Reinvent 4: Modern AI–driven generative molecule design. Journal of Cheminformatics, 16(1), 20.
Luukkonen, S., Meijer, E., Tricarico, G. A., Hofmans, J., Stouten, P. F., van Westen, G. J., & Lenselink, E. B. (2023). Large-scale modeling of sparse protein kinase activity data. Journal of Chemical Information and Modeling, 63(12), 3688-3696.
McNutt, A. T., Francoeur, P., Aggarwal, R., Masuda, T., Meli, R., Ragoza, M., … & Koes, D. R. (2021). GNINA 1.0: molecular docking with deep learning. Journal of cheminformatics, 13(1), 43.
Nahal, Y., Menke, J., Martinelli, J., Heinonen, M., Kabeshov, M., Janet, J. P., … & Kaski, S. (2024). Human-in-the-loop active learning for goal-oriented molecule generation. Journal of Cheminformatics, 16(1), 1-24.
Nigam, A., Pollice, R., Tom, G., Jorner, K., Willes, J., Thiede, L., … & Aspuru-Guzik, A. (2024). Tartarus: A benchmarking platform for realistic and practical inverse molecular design. Advances in Neural Information Processing Systems, 36.
Olivecrona, M., Blaschke, T., Engkvist, O., & Chen, H. (2017). Molecular de-novo design through deep reinforcement learning. Journal of cheminformatics, 9, 1-14.
Paul, S. M., Mytelka, D. S., Dunwiddie, C. T., Persinger, C. C., Munos, B. H., Lindborg, S. R., & Schacht, A. L. (2010). How to improve R&D productivity: the pharmaceutical industry’s grand challenge. Nature reviews Drug discovery, 9(3), 203-214.
Shahriari, B., Swersky, K., Wang, Z., Adams, R. P., & De Freitas, N. (2015). Taking the human out of the loop: A review of Bayesian optimization. Proceedings of the IEEE, 104(1), 148-175.
Stanley, M., Bronskill, J. F., Maziarz, K., Misztela, H., Lanini, J., Segler, M., … & Brockschmidt, M. (2021, August). Fs-mol: A few-shot learning dataset of molecules. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2).
van Tilborg, D., Alenicheva, A., & Grisoni, F. (2022). Exposing the limitations of molecular machine learning with activity cliffs. Journal of Chemical Information and Modeling, 62(23), 5938-5951.
Winter, R., Montanari, F., Steffen, A., Briem, H., Noé, F., & Clevert, D. A. (2019). Efficient multi-objective molecular optimization in a continuous latent space. Chemical science, 10(34), 8016-8024.